TL;DR

“Gradient descent” é um algoritmo de otimização. Ele é usado pra procurar mínimos de uma função de modo iterativo, dando passos em direção ao ponto “mais baixo” da função.

Gradient Descent

Quando a gente fala em “machine learning”, ou “aprendizado de máquina”, o que eles querem dizer com esse “aprender”? Como que se ensina uma máquina?

Ehh… não é bem assim. Bem menos sexy, na verdade, mas também mais simples.

O Setup

Como que nós podemos medir o quão bom o nosso modelo de machine learning é? Como comparamos dois modelos diferentes? Existe uma função que mede exatamente isso, uma função que mede o erro de cada modelo. Essa função aceita os parâmetros do modelo, e retorna o erro do modelo.

Nós temos que saber a derivada dessa nossa função de erro.

Por exemplo, se eu estou jogando curling eu não posso jogar o disco muito forte nem muito fraco. Eu tenho que jogar na força certa. Se eu conseguir formular uma função matemática que pega a força que eu joguei o disco retorna a distância da disco até o meu alvo, esse seria a função do erro, e eu seria o modelo.1

Aqui nós estamos tentando encontrar o parâmetro (no nosso exemplo a força) que vai reduzir o erro (distância) ao máximo. Mas como?

Encontrando o Mínimo

Essa pergunta não é nova. Desde o colegial nós aprendemos a achar mínimos e máximos de uma função. Mas e se nós tivermos várias variáveis? Poderíamos usar cálculo multivariável, resolvendo um sistema de equações com as derivadas parciais.

O problema é nós resolvemos essas equações simbolicamente - com variáveis simbólicas como $x$ e $y$. Mas isso é muito difícil para um computador. Algumas calculadoras até oferecem essa opção mas muitas vezes não encontra resultado. Uma solução mais robusta é resolver esse problema numericamente.

Além disso, resolvendo numericamente nós evitamos alguns problemas teóricos relacionados ao uso de derivadas de funções que não são contínuas.2

A Matemática

Resolver numericamente consiste em computar valores aproximados da nossa função do erro e iterativamente mudar os parâmetros de nossa função, reduzindo esse erro aos poucos (se está confuso, calma que vai ficar mais claro até o fim desse post). Antes, vamos definir nossos termos:

Fazendo aproximações e resolvendo numericamente, nós nunca chegamos de verdade no mínimo, mas chegamos bem perto dele. Ou seja, o resultado que temos também é uma aproximação do mínimo da nossa função.
  • f→f \rightarrow nossa função que indica o erro do nosso modelo
  • p→p \rightarrow o parâmetro da nossa função
  • e→e \rightarrow o erro do nosso modelo para esse parâmetro
∴f(p)=e\therefore f(p) = e

Vamos também supor para o nosso exemplo que nossa função seja concava, bonitinha, com um mínimo só. Alguma coisa assim:

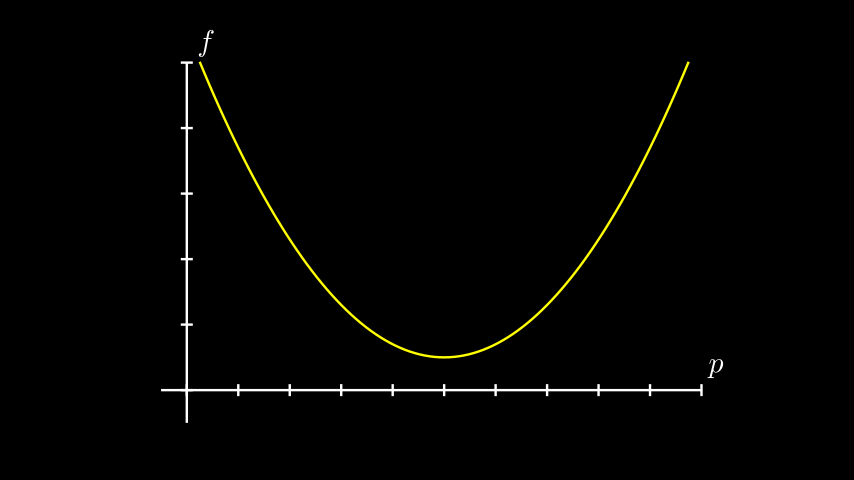
É importante perceber que uma função de erro é dificilmente assim. Em casos mais práticos a função é bem mais bagunçada e têm vários máximos e mínimos. E quando isso acontece, esses métodos vão aproximar um mínimo local, e não global.

Derivadas

Lembrando que uma derivada é o coeficiente angular de uma linha tangente à uma curva, se a gente “cai” num ponto aleatório da nossa função de erro, a gente percebe que:

  • Quando estamos “a frente” do nosso ponto mais baixo $\rightarrow$ nossa derivada é negativa
  • Quando estamos “pra trás” do nosso ponto mais baixo $\rightarrow$ nossa derivada é positiva

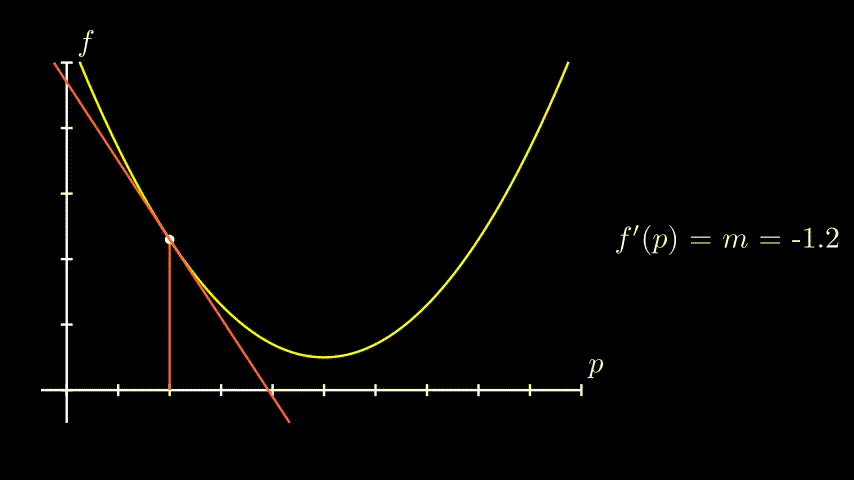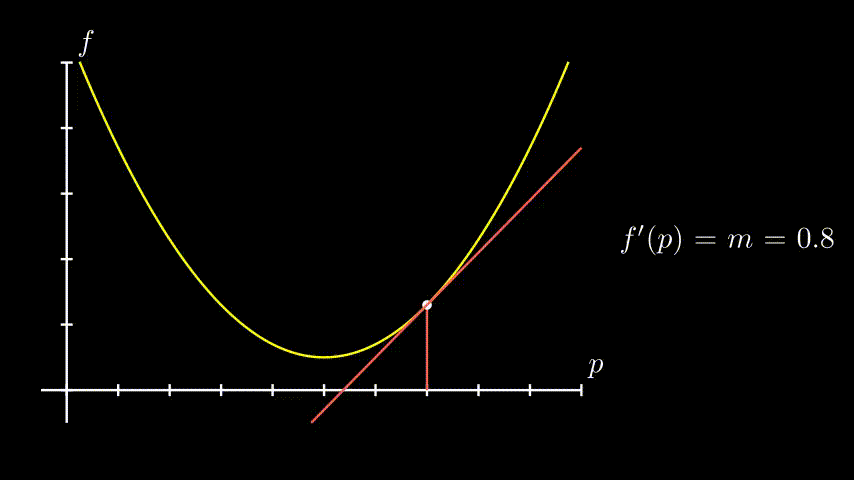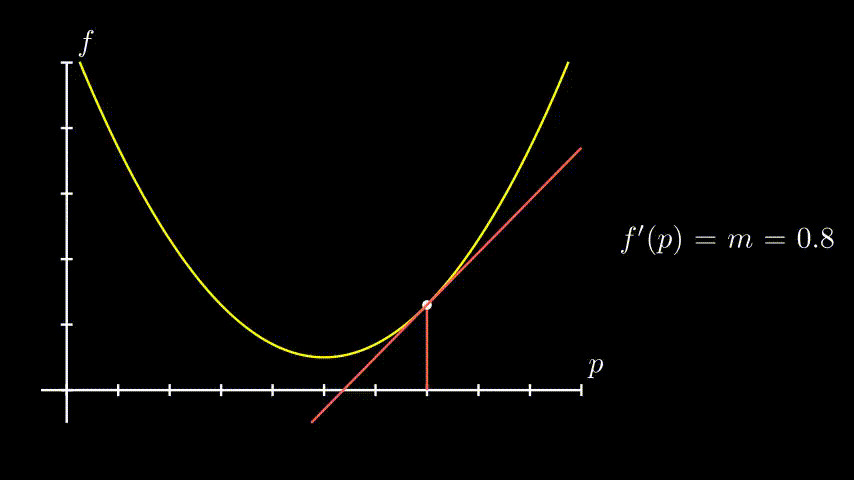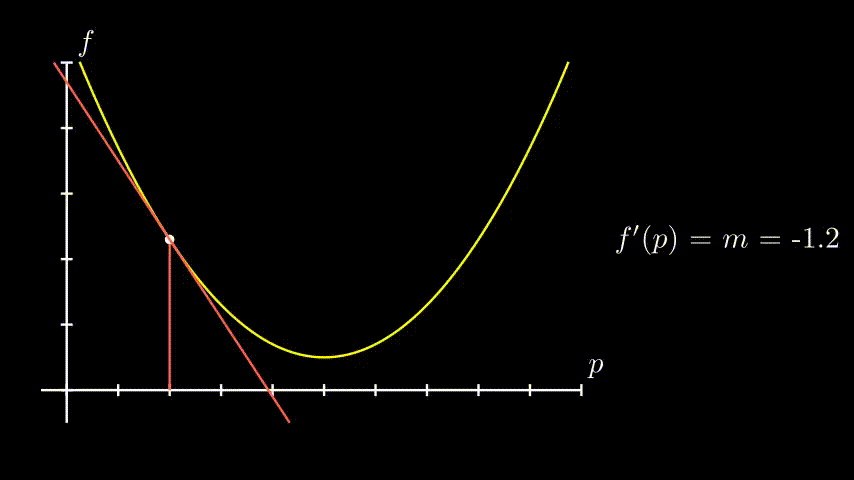
Ou seja, a derivada já nos indica pra que lado devemos caminhar. Mais tecnicamente, ela indica se o mínimo da nossa função está num valor maior ou menor do que o nosso $p$ atual!

Mais que isso, quando chegamos mais perto do mínimo nossa derivada também diminui. Ou seja, a magnitude da derivada também nos fala quão próximo desse mínimo nós estamos.

Passo a Passo - O Algorítmo

Agora nós podemos começar de um ponto aleatório e dar vários passinhos até chegar mais e mais perto do nosso mínimo. O nosso passo-a-passo fica assim:

  • Chuta aonde está o ponto mais baixo
  • Calcule a derivada da função nesse ponto
  • Ajuste o seu chute dando um passo em proporcional à derivada (na direção oposta)
  • Repita o processo até que esteja satisfeito

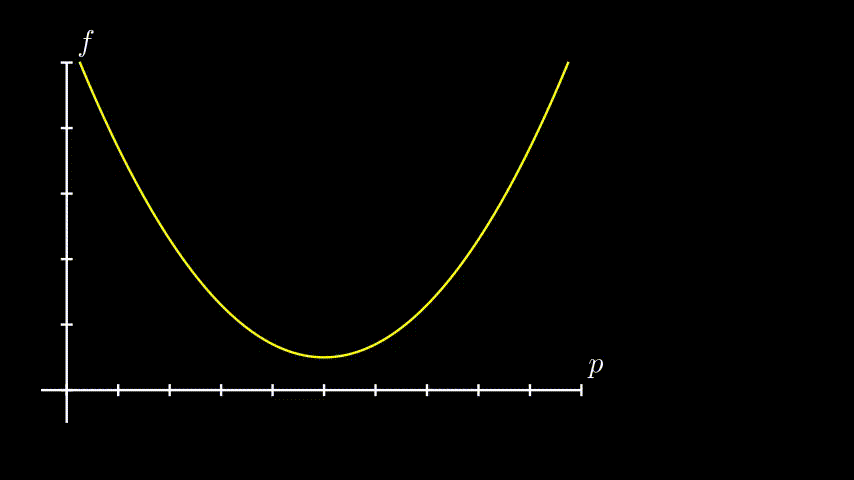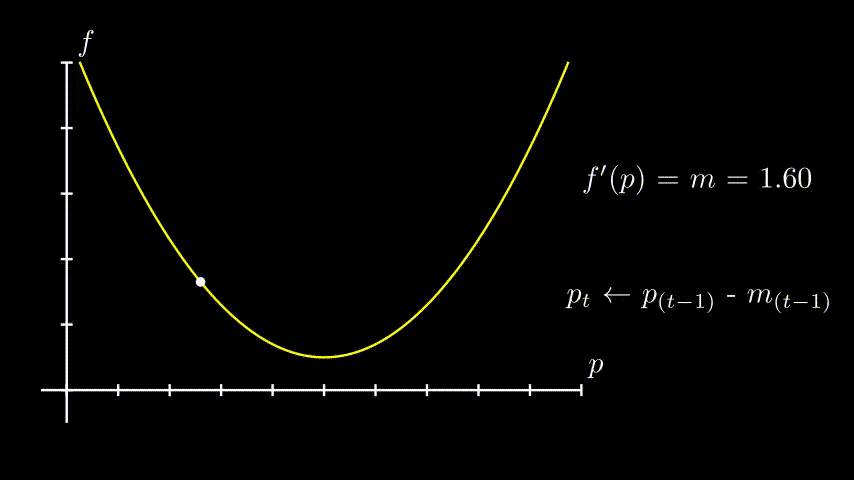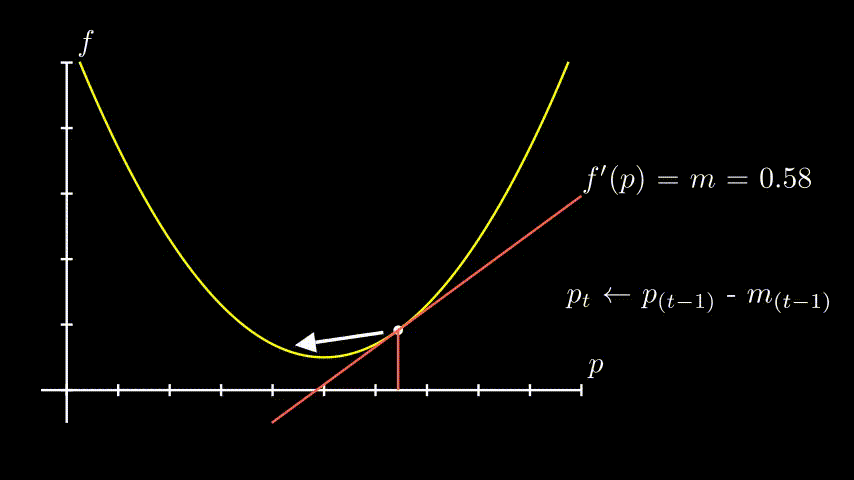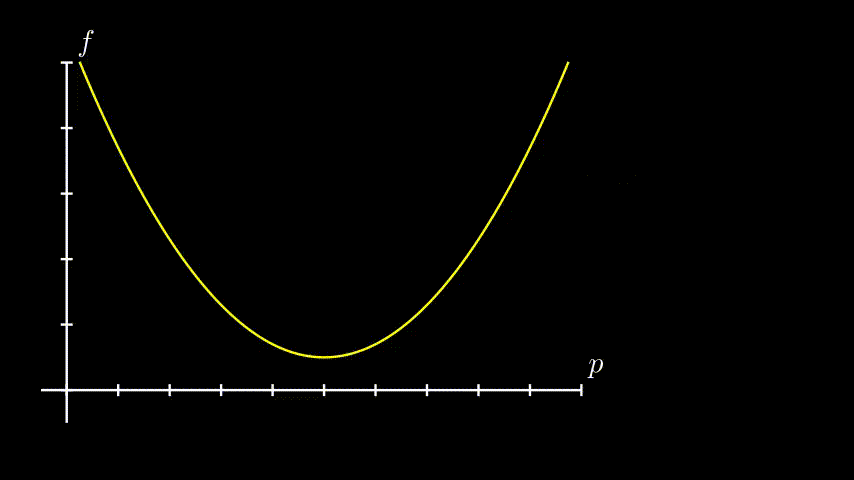
E é isso! A idéia básica é essa. O resto são detalhes de implementação.

Passo Maior que a Perna - Learning Rate

Mas e se a curva é muito íngreme e se nosso passo acaba sendo muito largo? E se a gente nunca consegue parar nesse mínimo porque sempre passamos dele?

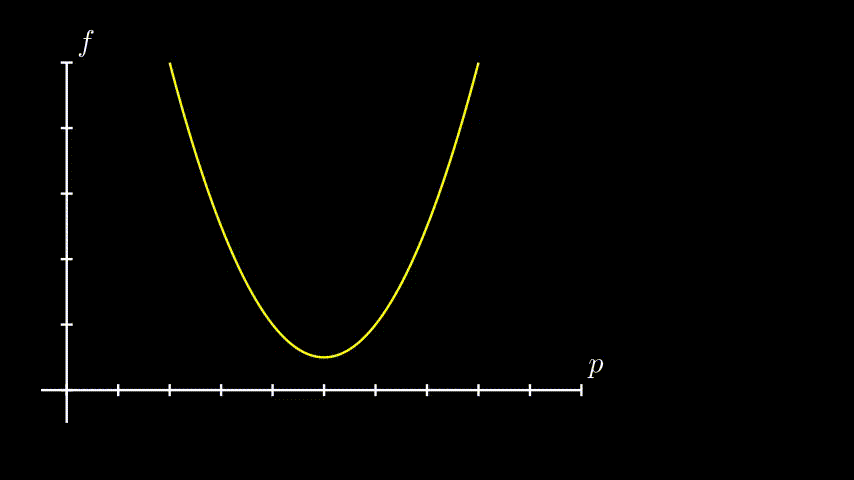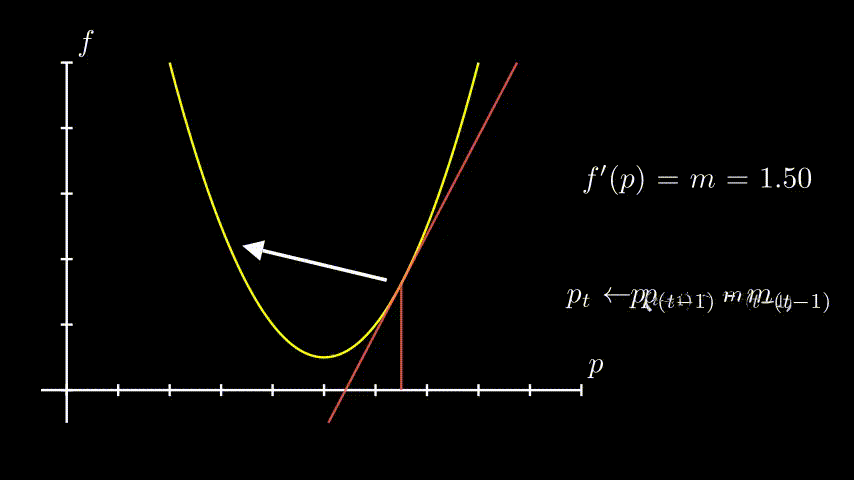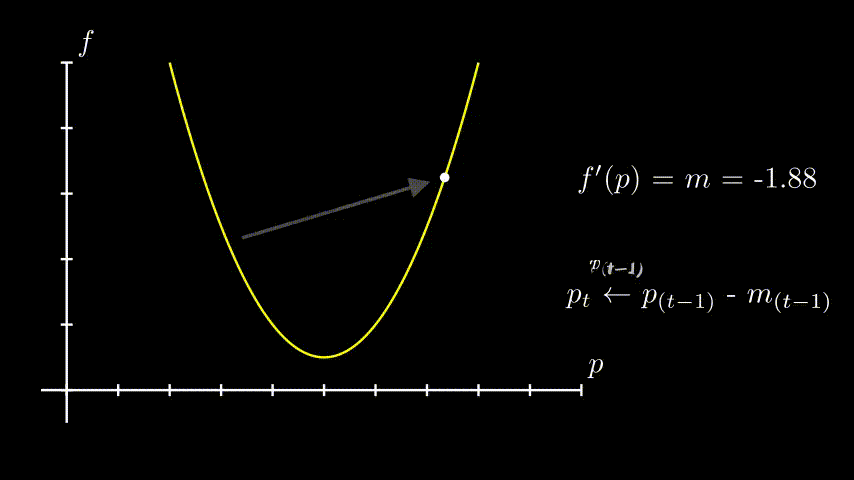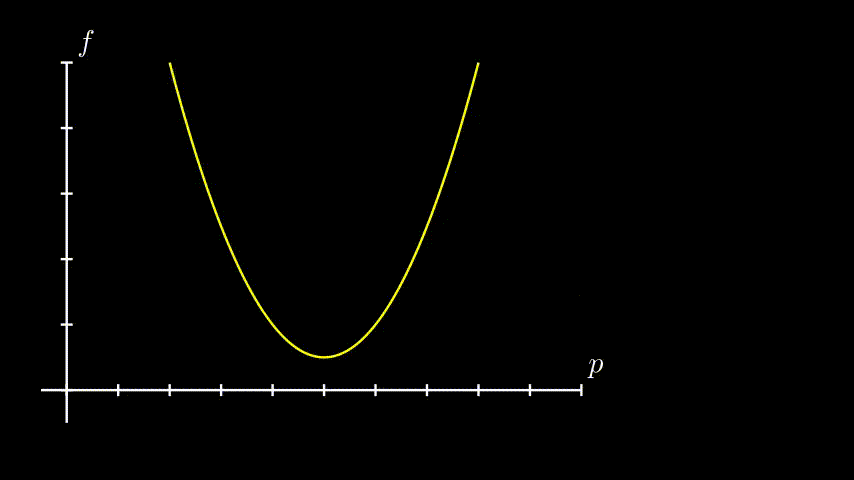
Nós podemos ajustar o passo, multiplicando por uma constante. Mas temos de tomar cuidado - se o passo for muito pequeno, talvez nunca chegaremos no mínimo (além de demorar muito mais do que o necessário) e se muito largo, e vamos acabar mais longe ainda. Como encontrar o essa constante? Tentativa e erro. Ao contrário do(s) parâmetro(s) da função, não encontramos esse valor através desse processo automatizado.

Essa constante é o que chamamos de learning rate (taxa de aprendizado, muitas vezes denominado $\alpha$), e é um hyperparâmetro do modelo. A equação então fica:

  • pt→p_{t} \rightarrow o “novo” parâmetro
  • pt−1→p_{t-1} \rightarrow o parâmetro anterior
  • α→\alpha \rightarrow uma constante que multiplicamos pela derivada, controlando o passo - a taxa de aprendizado
  • mt−1→m_{t-1} \rightarrow a derivada da função do erro, que é a linha tangente à função, computada no ponto $p_{t-1}$
pt←pt−1−αmt−1p_{t} \leftarrow p_{t-1} - \alpha m_{t-1}

Os parâmetros de um modelo são os valores que são otimizados nesse processo. Os hyperparâmetros de um modelo são valores que não são otimizados sistematicamente e devemos ajustá-los manualmente.

Mas os mesmos cuidados aplicam aqui. Essa constante não pode ser muito larga, nem muito pequena. Se muito grande, voltamos a dar passos muito largos, e vice-versa.

Várias Variáveis - O Gradiente

Por enquanto nós estamos olhando exemplos muito simples. Mas e se tivéssemos muitas variáveis no nosso modelo? A idéia é a mesma: computamos a derivada parcial em relação a cada uma dessas variáveis, e damos passos nessas direções. Quando empacotamos todas essas derivadas parciais, nós temos o gradiente da nossa função de erro! Dai que vem o nome gradient descent (ou descida do gradiente).

Em duas dimensões, podemos pensar na nossa função de erro como tentando encontrar o ponto mais baixo de uma cratera, num dia muito nublado - damos um passo pra onde a inclinação indica. Quanto mais íngrime, maior o passo que damos.

Inclusive, o gradiente de uma função sempre aponta pra direção de maior aumento. Se formos para o sentido oposto do gradiente, estamos indo na direção de maior declínio.

Ah, e a nossa linha tangente vira um plano tangente à curva!

Empacotando os parâmetros (um para cada dimensão) em um vetor, nos ficamos com:

  • pt⃗→\vec{p_{t}} \rightarrow os “novos” parâmetros (um para cada dimensão)
  • pt−1⃗→\vec{p_{t-1}} \rightarrow os parâmetros “anteriores” (um para cada dimensão)
  • ∇f(pt−1⃗)→\nabla f(\vec{p_{t-1}}) \rightarrow o gradiente da função do erro, que são as derivadas parciais de cada uma das dimensões do nosso problema, computadas no ponto $\vec{p_{t-1}}$
  • α→\alpha \rightarrow uma constante que multiplicamos pelo gradiente, controlando o passo - a taxa de aprendizado
pt⃗←pt−1⃗−α∇f(pt−1⃗)\vec{p_{t}} \leftarrow \vec{p_{t-1}} - \alpha \nabla f(\vec{p_{t-1}})

Eu sei que se você não está 100% confortável com álgebra linear isso pode assustar um pouco. Mas o que essa equação descreve são várias equações iguais à que apresentamos acima. Uma para cada dimensão do nosso problema. Ou seja:

  • d→d \rightarrow a dimensão do parâmetro
  • pt(d)→p_{t}^{(d)} \rightarrow o “novo” parâmetro da dimensão $d$
  • pt−1(d)→p_{t-1}^{(d)} \rightarrow o parâmetro anterior da dimensão $d$
  • α→\alpha \rightarrow uma constante que multiplicamos pela derivada, controlando o passo - a taxa de aprendizado
  • ∂∂pt−1(d)f(pt−1(d)))→\frac{\partial}{\partial p_{t-1}^{(d)}} f (p_{t-1}^{(d)})) \rightarrow a derivadas parcial da nossa função do erro para a dimensão $d$, em relação ao parâmetro anterior da mesma dimensão
pt(d)←pt−1(d)−α∂∂pt−1(d)f(pt−1(d))p_{t}^{(d)} \leftarrow p_{t-1}^{(d)} - \alpha \frac{\partial}{\partial p_{t-1}^{(d)}} f (p_{t-1}^{(d)})

Eu sei que ainda é muita letrinha, e que pode ser confuso. Respira fundo e vai com calma. Reveja isso quanto necessário e verifica que isso faz sentido. Quando falarmos de regressão linear isso também vai ficar mais claro.

“Aprendizado”?

Esse processo de reduzir o erro de um modelo é o que chamamos de “aprendizado”, ou como “ensinamos” do modelo!

Bom, eu sei que é meio decepcionante. Ninguém aprende assim. Mas calma, deixe-me explicar. em machine learning, essa função de erro é formulada a partir dos exemplos. Essa função muda de modelo para modelo.

No exemplo do começo do post, quando eu jogo curling, uma função de erro poderia ser a soma de todas as distâncias do centro do alvo até o meu disco. Ou seja, cada experiência minha é levada em consideração quando eu tento minimizar meu erro.

Quando seguimos as etapas desse algorítmo, cada passo é dado depois de computar a derivada. E a derivada leva em consideração todos as nossas tentatívas (exemplos)3. Ou seja, reduzimos o erro depois de “visitarmos” essas experiências passadas. Do mesmo jeito que eu, quanto mais vezes eu tento, vou melhorando (reduzindo meu erro).

Tudo depende de como definimos “aprender”. Se eu definir como “a melhora de performance com nossas experiências”, até faz sentido falar que a máquina aprende.

Além disso, quando falamos de stochastic gradient descent (descida do gradiente estocástico), ou online learning, nós visitamos uma parte dos exemplos pra cada passo, o que traz mais essa idéia de melhorar performance quando o modelo “vê” novas observações, e reforçando essa ideia de aprendizado.

Não vamos falar de stochastic gradient descent ou online learning nesse post. Aliás, existem muitas variações desses algoritmos de otimização. Na prática, ninguém acaba usando gradient descent desse jeito que eu expliquei por haver opções melhores, mas a idéia central de todos os algoritmos é a mesma.

Outras Implementações

Existem maneiras de melhorar a performance desses algoritmos. Por exemplo, nós poderíamos reduzir o learning rate a cada passo, usar uma idéia de momento, usar mais que apenas a primeira derivada, etc. Algum desses algorítmos são:

Não vamos explicar esses métodos nesse post. Mas cada um deles procura melhorar um aspecto do gradient descent, de uma maneira ou outra, mas todos tem suas ressalvas. As vezes eles acabam demorando mais pra chegar no nosso mínimo, ou então não conseguimos usá-los quando o número de dimensões aumenta, entre outros.

Nomenclatura

Nós falamos bastante dessa “função do erro”. Mas existem vários nomes que também são usados:

  • Função do erro (error function)
  • Função objetivo (objective function)
  • Função de custo (cost function)
  • Função de energia (energy function)
  • Função de perda (loss function)

Em todos os casos, nós procuramos o mínimo dessa função.

Além disso, nós falamos sobre “aprender”. Em machine learning, esse processo também é chamado por nomes diferentes:

  • Aprender (learn)
  • Treinar (train)
  • Ajustar (fit)

Explicamos o que são os parâmetros e os hyperparâmetros. Esse parâmetros são chamados de:

  • Parâmetros (parameters) - duh
  • Pesos (weights)

São diferentes nomes, mas eles se referem às mesmas coisas!

Footnotes

  1. Obviamente esse exemplo é muito simples. Existem muitos outros fatores que deveriam ser levados em consideração. Mas ainda assim esse é um problema comum em machine learning - muitas vezes existe bastante incerteza de que os dados obtidos possuem as informações necessárias para qualquer tipo de previsões. ↩

  2. Nossa função de erro não precisa ser diferenciável em todos os pontos. A função $f(x)=\mid x \mid$ por exemplo não é diferenciável quando $x=0$, mas como estamos resolvendo numericamente isso não é um problema (nunca vamos cair no ponto $0.00000…0$, mas talvez no $0.00000…1$, etc.). Mesmo que fosse, nós poderíamos, se quiséssemos, definir uma “derivada” no ponto $x=0$. ↩

  3. Para ver mais sobre como formulamos essas funções de erro (custo) a partir de nossas observações, veja um exemplo sobre regressão linear ou regressão logística. ↩